(c) 2002 Gabriel Dunne

Original Document: color/shape/sound

Introduction

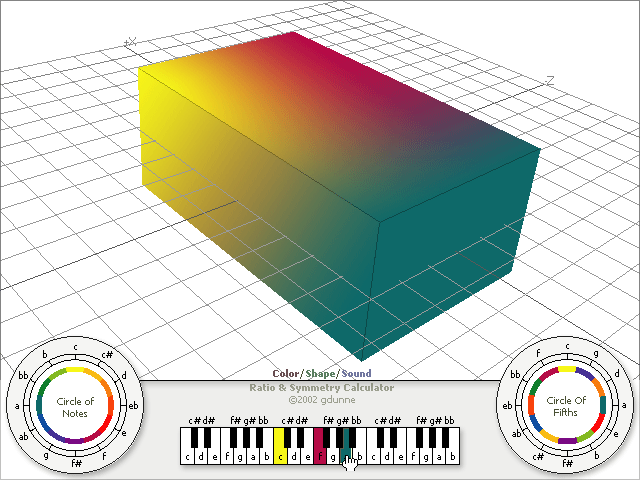
The Color/Shape/Sound explorer generates a three-dimensional shape as a result from musical input from the user. The calculator attributes color to certain notes, creating a harmonious relationship between Shape, Color and Sound.

The Circle of Fifths

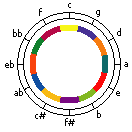
The Circle of Fifths is a way to learn the key of a given 12-note-scale musical composition. The Circle of Fifths tells you how many sharps or flats are in a given key. The key of C has no sharps or flats, for example. The diagram is called the Circle of Fifths because as you go clockwise you go up a fifth. For example, the fifth note of the C major scale is G. The fifth note of the G major scale is D, and so on.

Notice that every other note is succeeded by the one before. C, skip G, D, skip D, A, etc. Also notice how there are twelve notes corresponding to twelve numbers on a clock. C is in he 12 noon position. G is in the 1 o’clock position (likewise has one sharp; F in the 11 o’clock position.) D is in the two o’clock position (likewise has sharps; F and C). A is in the 3 o’clock position (likewise has 3 sharps; F, C, G). E is in the four o’clock position and has 4 sharps (F, C, G, D). B is in the 5 o’clock position and has 5 sharps (F,C,G,D,A). F# is in the 6 o’clock position and has 6 sharps (F,C,G,D,A,E; everything is sharp except B; notice also how this corresponds with the key of F in which it has one flat, Bb). If you follow the gray lines of the inner star, you can visually see how a single octave of sound is represented in this circular fashion.

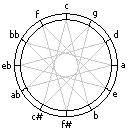
As we move clockwise around the wheel, we begin to see a pattern of the amount of sharps contained in each major key. There are no sharps in the key of C. There is one sharp in the key of G, and two in the key of D, etc.

C :
G : F#
D : F#, C#
A : F#, C#, G#
E : F#, C#, G#, D#
B : F#, C#, G#, D#, A#
F#: F#, C#, G#, D#, A#, E#
C#: F#, C#, G#, D#, A#, E#, B#

To count the number of flats, we move counterclockwise along the wheel. There are no flats in the key of C, one in the key of F, two in the key of Bb, etc. Because it’s neater, we write everything as flats.

C :
F : Bb
Bb: Bb, Eb
Eb: Bb, Eb, Ab
Ab: Bb, Eb, Ab, Db
Db: Bb, Eb, Ab, Db, Gb
Gb: Bb, Eb, Ab, Db, Gb, Cb
Cb: Bb, Eb, Ab, Db, Gb, Cb, Fb

The Circle of Notes

The Circle of Notes is something I came up with to describe arranging the notes chromatically around a circle. The only relationship between the notes is the actual distance in which they are spaced from each other on the keyboard. C is spaced away from C# the same distance as A is spaced from Bb, etc. Hence, the Circle of Notes is simply a representation of a single octave wrapped to 360 degrees.

The Color Wheel

The Color Wheel describes the relationships between colors. It is laid out so that any two primary (red, yellow, blue) are separated by the secondary colors (orange, violet, and green).

The Color Wheel In Relation to the Circle of Notes

When we composite the Color Wheel behind the Circle of Notes, we can create a working relationship between the two. As we move along the wheel clockwise, we can relate specific notes to specific colors, eventually looping through an octave will also loop through the entire spectrum of color.

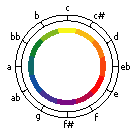
According to this model, C relates to Yellow. E relates to Red, and Ab relates to Blue, (the primary colors). If we look at these notes on a keyboard, we can see that they are spaced two tones (steps) apart, or four semi-tones (half steps) apart. An octave consists of twelve semi-tones total, so four semitones is an exact third of an octave. Exactly the same relationship that the primary colors have to the color wheel – they are spaced apart in perfect thirds. By this model, C, E and Ab are the ‘primary notes’ of the octave.

If we rearrange the notes on the Circle of Notes so that the wheel becomes the Circle of Fifths, and let the corresponding colors follow the move, the result is a very dissonant color wheel:

According to this model, a very interesting relationship is illustrated, simply because of the dissonance between certain notes. Complimentary colors stay in the same, but their arrangement in a circular fashion is distorted to follow the Circle of Fifths model.

Secondary Colors In Relation to the Circle of Notes

The notes in between the ‘primary notes’ then represent the secondary and tertiary colors represented in the color wheel.

While the keyboard is beginning to look more like Fisher-Price, we begin to notice a definite pattern and relationship. As we move up and down the octaves of the keyboard, the color wheel loops 360 degrees, managing to assign a specific color to each note in the octave.

Notes, and Their Relationship to Ratio & Symmetry

Pythagoras observed that when the blacksmith struck his anvil, different notes were produced according to the weight of the hammer. Number (in this case "amount of weight") seemed to govern musical tone. Further, he observed that if you take two strings in the same degree of tension, and then divide one of them exactly in half, when they are plucked the pitch of the shorter string is exactly one octave higher than the longer:

Again, number (in this case "amount of space") seemed to govern musical tone. Or does musical tone govern number? He also discovered that if the length of the two strings are in relation to each other 2:3, the difference in pitch is called a fifth:

…and if the length of the strings are in relation to each other 3:4, then the difference is called a fourth.

Thus the musical notation of the Greeks, which we have inherited can be expressed mathematically as 1:2:3:4

All this above can be summarized in the following, with some other additional ratios and their names:

		Whole Note		1:1
Diapason		Octave		2:1
Diapason Diapente		1.5 Octaves		3:1
Disdiapason		2 Octaves		4:1
Diepente		The 5th		3:2
Biatessera		The 4th		4:3
Tonus		Whole Tone		9:8

Represented visually:

Whole Note (1:1) :
Diapason (2:1) :
Diapason Diapente (3:1) :
Disdiapason (4:1) :
Diepente (3:2) :
Biatessera (4:3) :
(5:4) :
(4:9) :
Tonus (9:8) :

Notes, and Their Relationship to Ratio & Symmetrym, Combined with the Relationship of Color.

To develop an interface that would allow interaction between shape, color and tone involves an initial choice. Which aspect would the user interact with? Would they chose colors and have the program draw a shape, and play the relating sound? Would the user draw a shape, and have the program chose the appropriate color in the relationship, and play the corresponding notes? The third possibility would be to have the user play a piece of music, and have it relate directly to shape and color. I have decided that this will be the initial implementation of the first version of this application.

Essentially, the user will play a sequence of notes, the program will calculate the ratios between these notes and draw a shape, as well as attribute each note to a corresponding color on the color wheel.

In the future, it’s possible that additional versions of the program will allow the user to interact with all three, and see how the different factors of shape, color, and sound relate to each other no matter which aspect is modified.

Interface Design

Initial concepts of interface design include implementation of both color/note wheels, and an interactive keyboard. The large area above will contain the form that results from the ratios designated by the notes played on the keyboard.

The shapes drawn must be cubic in order to relate to the ratios in three dimensions, but future implementation in other geometries will be possible.

In this demonstration, the user picked the notes C, F and A in succession, drawing a cube that relates to the ratios of space that exists between the notes, and coloring the cube appropriately. If the user was to hit a fourth note, it will override the first note pressed in the sequence. In this case, if the user decides to hit D, it will override C, and change the yellow to orange, as well as change the shape of the cube.